Before I move on to trying more complicated things that I would do with MATLAB (e.g. 3D plotting), I want to learn the basics of the thing I would like to do on R, namely data crunching and visualization.

For that I will use mtcars database because:

• It’s simple.
• It’s standard.
• Flowers are boring.
• Saddly, there’s no simple, standard, motorcycles database.

So first I need to load the Pandas library. This library will introduce the DataFrame object much like R’s own data.frame.

import pandas as pd

There’s a package that brings RDatasets to Python, but I saved mtcars as a CSV (comma separated values) file because reading my own data from Python is a very important step. Which by the way is very easy:

cars = pd.read_csv("mtcars.csv")

To print what I just read, there’s a head function. It will shows us the first bunch of rows. head(n) will give you the first n rows, but let’s use the default.

cars.head()

We can see that there’s no name for the first column. We could add a name like “carname”, but in this case the name of the car represents a single row, so maybe we should use it as a name for the row instead of just $1,2,3,\dots$

cars = pd.read_csv("mtcars.csv",index_col=0)
cars.head()

If you happen to know the dataset, you’ll notice that I changed the variable am from binary to text. I did this to explore pandas use of categorical data from text.

Speaking of that, let’s see how the data was saved in our variable.

cars.info()

<class 'pandas.core.frame.DataFrame'>
Index: 32 entries, Mazda RX4 to Volvo 142E
Data columns (total 11 columns):
mpg     32 non-null float64
cyl     32 non-null int64
disp    32 non-null float64
hp      32 non-null int64
drat    32 non-null float64
wt      32 non-null float64
qsec    32 non-null float64
vs      32 non-null int64
am      32 non-null object
gear    32 non-null int64
carb    32 non-null int64
dtypes: float64(5), int64(5), object(1)
memory usage: 3.0+ KB

We can see some important data on the…data (Metadata?). How each variable is stored and the memory size of the DataFrame. This is a really small dataset, but with bigger files this would be more and more important to be aware of.

Other function that seems very useful is describe, which summarizes the columns in the most standard statistics: count,mean, standard deviation and quartiles.

cars.describe()

As a shortcut for visualization, there’s another cool feature of pandas: we can call plot directly to the DataFrame. This allows to plot a histogram (or whatever) of some columns directly to see what we are doing. For this we need the plotting library.

import matplotlib.pyplot as plt
%matplotlib inline

To select a single column of our data, pandas uses []. So for example we can get the mpg variable and get the histogram right out of the DataFrame object with:

cars['mpg'].hist()
plt.show()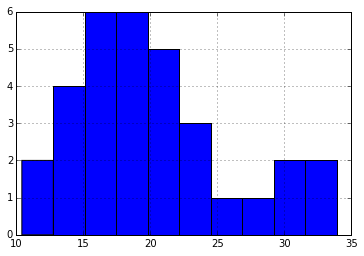

Now we can visualize some pandas functionality. For example, we can easily group by type of transmission using the groupby function. I take cars, select the columns ‘mpg’ and ‘am’, then apply the groupby function to tell pandas I want to group by ‘am’, and that I want to summarize the rest using the function mean. Finally I plot it.

cars[['am','mpg']].groupby('am').mean().plot(kind='bar')
plt.show()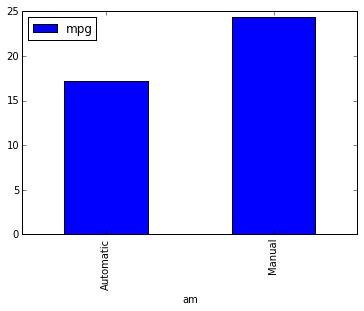

How about a scatter plot? Maybe I would want to see the relationship between miles per gallon vs the horse power.

plt.scatter(cars['mpg'],cars['hp'])
plt.show()

What about beautiful plots?

By this time some may be missing ggplot because of its elegant style. Well, matplotlib has different possible styles, included the beloved ggplot, only by setting style.use

plt.style.use('ggplot')
plt.scatter(cars['mpg'],cars['hp'])
plt.show()

There is also another library called seaborn that brings new styles to matplotlib and more visualization functions. It doesn’t come with the Anaconda distribution, but it’s really easy to get. You just open a terminal (cmd/powershell on windows), type conda install seaborn and you’re done. Now you just load it to get more beautiful plots and can begin to use fun plots like the regplot, which performs linear regression directly in the plot. Plot, plot. I’m setting the figure size because seaborn figures come out a little bigger and

import seaborn as sns
plt.figure(figsize=(5, 4))

sns.regplot('mpg','hp',data=cars)

<matplotlib.axes._subplots.AxesSubplot at 0xc96cc88>

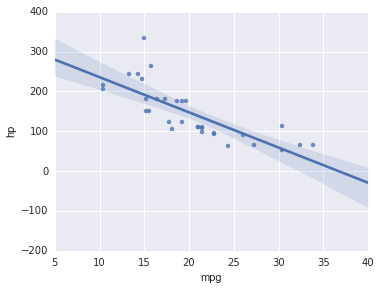
The dependence doesn’t seem to be linear, let’s try a polinomial regression.

plt.figure(figsize=(5, 4))
sns.regplot('mpg','hp',data=cars,order=2)

<matplotlib.axes._subplots.AxesSubplot at 0xc679908>

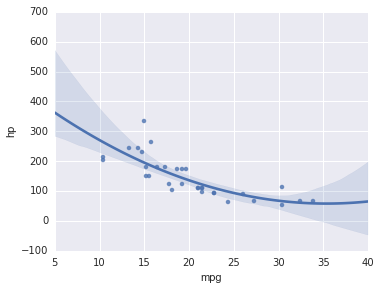
One of the things I didn’t like about R, or more specifically R on Windows, is that plots don’t seem to have any anti-aliasing. I haven’t had that problem in Python, although you wouldn’t notice anyway since these graphs are all un PNG format now, which would look equally great if I generated them in R. I took a screenshot with an equivalent plot generated in RStudio:

library(ggplot2)

cars <- mtcars

ggplot(data = cars, aes(x=mpg,y=hp)) + geom_point() + 
  stat_smooth(method="lm",formula = y ~ poly(x,2,raw=TRUE))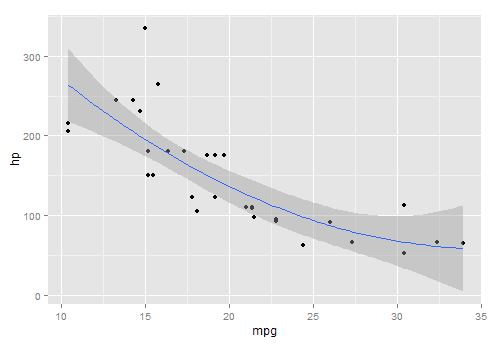

Look at that horrible line!

If you have a workaround for turning on antialiasing on R for Windows I would very much appreciate it, since I’ve searched hungrily for it.

There’s a ggplot library for Python too, although I read that it is a little buggy still. It would be really convenient to use the same graphic language when moving between Python and R. I needed to install it too by running pip install ggplot in the terminal. Notice that the gsize variable is just format and it’s not necessary.

from ggplot import *
gsize = theme_matplotlib(rc={"figure.figsize": "5, 4"}, matplotlib_defaults=False)

ggplot(aes(x='mpg',y='hp'),data = cars) + geom_point() + gsize

<ggplot: (-9223372036841740621)>

I dropped the stat_smooth because there’s no way to specify the model yet, apparently. Anyway there it is.

Remember that you can get this IPython Notebook and others at my Github Page.

In the last post I defined a function that perform simulations for the birthday candle problem. This time I want to use it to visualize what happens if I change the parameters of the problem by using this function:

import numpy as np

def candles(n,M):
	Kj=np.zeros(M)
	for j in range(0,M):
		ni=n
		k=0
		while ni>=1:
			ni=ni-np.random.random_integers(1,ni)
			k+=1
		Kj[j]=k
	return np.mean(Kj)

There are several libraries for the things I will do here today (plotting and modelling), but today I’ll use the most straightforward ones. In later posts I plan to learn and write about the other libraries more specifically.

Plotting

I need to load another library, which is the “standard” one for plotting and it’s called matplotlib. (The second line is for the graphs to appear inside the notebook instead of in a new window but I’ll leave it in case someone is using IPython too).

import matplotlib.pyplot as plt
%matplotlib inline

Let’s begin by generating for candles from $1$ to $500$ and sampling 5 times.

M=5
N=500

K=np.zeros(N)
for n in range(1,N+1):
	K[n-1]=candles(n,M)

For plotting, you “create” the plot, then make customizations (like labels and colors), and then you show it.

plt.plot(K)
plt.ylabel('Rounds')
plt.xlabel('Candles')
plt.show()

Nice enough. But looks kinda noisy. I’ll change the number of samples per run to $M=1000$.

M=1000
N=500

K=np.zeros(N)
for n in range(1,N+1):
	K[n-1]=candles(n,M)

plt.plot(K)
plt.ylabel('Rounds')
plt.xlabel('Candles')
plt.show()

It looks kinda logarithmic. But don’t trust my word for it, lets see the graph of the natural logarithm.

plt.plot(np.log(range(1,500)),'r')

That means we could try to adjust a linear model to the exponential of $K$.

Modelling

First let’s see that $e^K$ looks indeed linear:

plt.plot(np.exp(K),label="Exp(K)")
plt.ylabel('Exp(Rounds)')
plt.xlabel('Candles')
plt.show()

Now we need a library for statistical modelling, so lets call scipy and it’s stats package.

from scipy import stats as stat

Now I’ll perform linear regression on $e^K$. This means that I’m trying to find numbers $a,b$ such that $e^K = a\times n+b$ plus some noise.

lin_K = stat.linregress(range(1,N+1), y=np.exp(K))
print(lin_K)

LinregressResult(slope=1.7974155631156676, intercept=-1.2491890297652617, rvalue=0.99070255893402914, pvalue=0.0, stderr=0.011060517470059619)

It seems it didn’t crash, so let’s try to plot it.

plt.plot(np.exp(K),label="Average rounds")
plt.plot(lin_K.intercept+lin_K.slope*range(1,N+1),label="Lin_model",color='r')
plt.ylabel('Average rounds')
plt.xlabel('Candles')
plt.legend(loc=4)
plt.show()

Pretty neat, although I would prefer a linear regression function with some kind of predict function or fitted values but I’ll leave that for other post.

Final graph and thoughts

By transforming back to the logarithm I get the final product:

plt.plot(K,label="Average rounds")
plt.plot(np.log(lin_K.intercept+lin_K.slope*range(1,N+1)),label="Lin_model",color='r')
plt.ylabel('Average rounds')
plt.xlabel('Candles')
plt.title("Rounds ~ log(%s + %s * Candles)" % (lin_K.intercept,lin_K.slope))
plt.legend(loc=4)
plt.show()

Remember that you can get this IPython Notebook and others at my Github Page.

I’ve never liked learning languages (programming or otherwise). The way I learned english and any phrase I know from any other language (elen sila lumenn omentielvo!) is by watching movies or reading books/blogs. As for programming languages, I have learned by having to solve problems so I’ll do just that. In these initial posts I’ll learn by hitting walls and finding the most straightforward tools to break them. After that I’ll try to find the standard practices for them.

The birthday candle problem

I follow Brent Yorgey’s The Math Less Traveled and I’ve just read his post on The birthday candle problem, as it sounds fun I decided to start my first introduction to Python by trying to run some simulations from it. You can read more about it on his post, but I’ll quote him on the problem:

A birthday cake has $n$ lit candles. At each step you pick a number $1 \leq k \leq n$ uniformly at random and blow out $k$ candles. If any candles remain lit, the process repeats (using a new value of $n$). As a function of $n$, what is the expected number of rounds needed to blow out all the candles?

I began this blog by saying that I wanted first of all to replace my need of MATLAB, so what I did was first to write some MATLAB code and I’ll try to reproduce it. I wrote the most straightforward code I came up with. Here it is:

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% PARAMETERSOF THE SIMULATION %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
obs=100; % Number of observations to estimate expected value for each n
N=300; % Max number of candles


%%%%%%%%%%%%%%%%%%%%%%
% PART 1: SIMULATION %
%%%%%%%%%%%%%%%%%%%%%%
K=zeros(N,1); % For storing the expected values

for n=1:N % Iterate for each number of candles
    ki=0; % To save number of rounds
    for j=1:obs % Generate observations
        ni=n;
        k=0; % Number of steps in this observation
        while ni>0 % Keep doing while there are lit candles
            k=k+1; % Add one more step
            ni=ni-floor((rand()*ni))-1; % Blow candles!
        end
        ki=ki+k; % Sum of rounds
    end
    K(n)=ki/obs; % Average rounds for this number of candles
end

%%%%%%%%%%%%%%%%%%%%
% PART 2: PLOTTING %
%%%%%%%%%%%%%%%%%%%%
plot(K) % Plot the estimates of expected value
hold on

%%%%%%%%%%%%%%%%%%%%%
% PART 2: MODELLING %
%%%%%%%%%%%%%%%%%%%%%
aaa=fitlm(1:N,exp(K)); % Fit a linear model to exp(k) (believe me, it looks logaritmic)

% FINAL PLOT
plot(1:N,log(aaa.Fitted)) % Fit fitted values (believe me, it looks great)
xlabel('n')
ylabel('Average rounds')

I put it for reference for those who would like to run it. Now the quest to find everything I need begins.

It seems that if I want to do numeric stuff I need to load a certain library called numpy. It’s my first library load. Yay!

##################
import numpy as np
##################

Random numbers

If I want to blow out candles I need some random numbers. Inside numpy, there’s this thing called random that has a function called random_integers that can generate some sequence of random numbers exactly how I need: given some $n$ generate a number between $1$ and $n$. I’ll work with $n=10$.

##################
n = 10
print(np.random.random_integers(1,n,))
##################

7

To see it better lets generate 5 numbers.

##################
print(np.random.random_integers(1,n,5))
##################

[ 1  8 10  6  4]

It looks kinda…long. Maybe later I’ll learn some way to clean it up.

Loops

Anyway now I have some random numbers and need a while loop to keep blowing out candles until there’s none left.

##################
n=10
k=0
while n>=1:
    k+=1
    r=np.random.random_integers(1,n)
    print("Round %s: From %s candles, I blow out %s." % (k,n,r))
    n=n-r
##################

Round 1: From 10 candles, I blow out 5.
Round 2: From 5 candles, I blow out 1.
Round 3: From 4 candles, I blow out 3.
Round 4: From 1 candles, I blow out 1.

Now lets make $M$ simulations to get an estimate of the expected value via the mean. Here, range(min,max) generates a sequence of numbers $min, min+1,\dots,max-1$

##################
n=10
M=4
Kj=np.zeros(M)

for j in range(0,M):
        ni=n
        k=0
        while ni>=1:
            ni=ni-np.random.random_integers(1,ni)
            k+=1
        Kj[j]=k
print(Kj)
print("The average is: %s." % np.mean(Kj))
##################

[ 3.  5.  2.  2.]
The average is: 3.0.

Functions

Now I’ll define it as a function to call it easily by the number of initial candles $n$ and the number of simulations $M$.

##################
n=10
M=4

def candles(n,M):
    Kj=np.zeros(M)
    for j in range(0,M):
        ni=n
        k=0
        while ni>=1:
            ni=ni-np.random.random_integers(1,ni)
            k+=1
        Kj[j]=k
    return np.mean(Kj)

K = candles(n,M)
print("With %s candles and a sample size of %s, I needed %s average rounds." % (n,M,K))
##################

With 10 candles and a sample size of 4, I needed 4.0 average rounds.

With this I can easily make simulations for lots of values of $n$. Let’s try for $n=1,2,\dots,10$ with a sample size of $M=1000$.

##################
M=1000
N=10

K=np.zeros(N)
for n in range(1,N+1):
    K[n-1]=candles(n,M)
    print("With %s candles, I needed %s rounds on average." % (n,K[n-1]))
##################

With 1 candles, I needed 1.0 rounds on average.
With 2 candles, I needed 1.527 rounds on average.
With 3 candles, I needed 1.849 rounds on average.
With 4 candles, I needed 2.037 rounds on average.
With 5 candles, I needed 2.261 rounds on average.
With 6 candles, I needed 2.41 rounds on average.
With 7 candles, I needed 2.613 rounds on average.
With 8 candles, I needed 2.684 rounds on average.
With 9 candles, I needed 2.794 rounds on average.
With 10 candles, I needed 2.996 rounds on average.

Now I’ve completed part 1 of the code. In the next post I’ll plot and model the data.

Remember that you can get this IPython Notebook and others at my Github Page.

Im not a savvy programmer. My background is in applied math and I’m mainly interested in data analysis, probability, combinatorics and linear optimization. Most of these disciplines require programming, but I prefer to concentrate more efforts in model design than in algorithm development.

For the past three years I’ve been using MATLAB in my job and my thesis, so I’m quite attached to it’s syntax and find it’s plots both beautiful and simple. I am well aware of it’s limitations for data analysis too (non-numeric data, anyone?), and I had learned to live with it. But I’ve changed jobs since and there’s the license cost, so that’s a little sad.

On the other hand there’s R, which I’ve been using sporadically since I got out of college. This summer I got back to it and got fairly familiar with all the Rmigthy Wickham features such as dplyr,tidyr and of course ggplot2. This is what I’ve been using in my workflow for the past months and I’ll most probably continue to use it for the foreseeable future, but for some reason I’m not enjoying it.

So my mind turned to this thing called Python that I had read that is a thing –specially on John D. Cook’s awesome The Endeavour which you should read– and I was thinking about learning. I had been reading a little bit when I realized that the name came from Monty Python; suddenly I was set on getting started.

I began searching for the best approach and decided to watch the nice history lesson from Scipy 2015 conference given by Jake VanderPlas in July –awesome timing.

It caught my attention the emphasis on Python as a MATLAB killer wannabe by the creators of some of the libraries.

Anyway, by the time I finished watching this I knew the path I had to take. So I went on to install the mentioned Anaconda distribution that seems to have all the libraries needed for a good head start on data analysis (scipy), machine learning (scikit-learn), numerical stuff (numpy), plotting (matplotlib), etc. Installation is completely painless (I installed in Windows and Linux) and you can start right away.

I started with this thing called IPython Notebook, or Jupyter, which is really awesome and I’m actually writing this post on it. Jupyter is a Markdown interface, so that means there also $\LaTeX$ code!

Really, that’s it. You just install the distribution, start IPython Notebook and click on “New”. When you do, say Hello for me.

print("Hello Python!!")

Hello Python!!

Since –for now– I’m not really interested in Python as a programming language but as a scientific tool, in the next post I’ll go directly into some libraries and start working on a problem.